صحنه آرایی (چیدمان صحنه) – قسمت دوم: مختصات هندسی
در ریاضیات، دستگاه مختصات کارتزین، یا مستطیلی یا دکارتی، برای مشخص کردن هر نقطه منحصر به فرد در صفحه یا فضا به کار میرود. برای مثال، در صفحه، نقطه با دو عدد مشخص میشود که معمولاً مختصه xx و مختصه yy آن نامیده میشوند. برای تعریف مختصات، دو خط مستقیم قائم یا عمود بر هم (محور xx یا افقی و محور yy یا عمودی) با زیربازههای واحد تعیین شدهاند (شکل ۱).
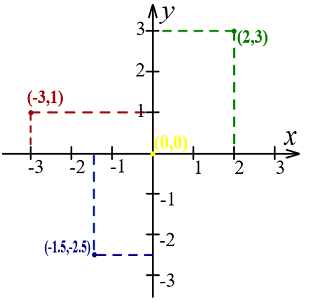
از دستگاه مختصات دکارتی، در فضا (با سه محور مختصات) و بُعدهای بالاتر نیز استفاده میشود.
با استفاده از دستگاه مختصات دکارتی، اشکال هندسی (مانند منحنیها) را میتوان با معادلات جبری توصیف کرد. برای مثال، دایرهای به شعاع ۲۲ را میتوان با معادله x2+y2=4x2+y2=4 بیان کرد (شکل ۲).
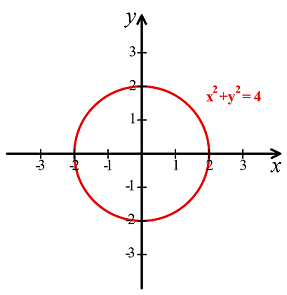
تاریخچه
نام مختصات دکارتی، به ریاضیدان و فیلسوف فرانسوی، رنه دکارت (René Descartes) بر میگردد که در کنار سایر کارهای علمیاش، برای ترکیب جبر و هندسه اقلیدسی تلاش کرد. این کار، تأثیر مهمی در هندسه تحلیلی، حسابان و نقشهکشی داشت.
ایده دستگاه مختصات در سال ۱۶۳۷ در دو مورد از نوشتههای دکارت معرفی شد. در نوشته دوم، دکارت ایده جدیدی برای مشخص کردن موقعیت یک نقطه یا جسم روی سطح با استفاده از دو محور متقاطع به عنوان ابزار اندازهگیری ارائه کرد.
دستگاه مختصات دکارتی دو بعدی
یک دستگاه مختصات دو بعدی، معمولاً از دو محور تشکیل میشود که نسبت به هم عمود هستند و صفحهای را تشکیل میدهند که صفحه xyxy نامیده میشود. محور افقی معمولاً با xx و محور عمودی با yy نمایش داده میشود. در دستگاه مختصات سه بعدی، یک محور دیگر که با zz نامگذاری میشود برای اندازهگیری بعد سوم فضا به کار میرود.
محورها معمولاً عمود نسبت به هم تعریف میشوند. در گذشته، از محورهای مایل نیز استفاده میشد که نسبت به یکدیگر زاویه قائم نداشتند. امروزه نیز در برخی از موارد خاصِ نظری از دستگاه مختصات با زوایای مایل نسبت به هم استفاده میشود.
همه نقاط دستگاه مختصات دکارتی یا کارتزین، با هم صفحه کارتزین را تشکیل میدهند. معادلاتی نیز که از دستگاه مختصات کارتزین استفاده میکنند، معادلات کارتزین نامیده میشوند.
نقطهای که محورها یکدیگر را قطع میکنند و با هم اشتراک دارند، «مبدأ» نامیده شده و با OO نشان داده میشود. محورهای xx و yyصفحهای را تعریف میکنند که صفحه xyxy نام دارد. هر محور نیز با فواصل واحد درجهبندی میشود که یک شبکه را تشکیل میدهند.
برای مشخص کردن یک نقطه خاص در دستگاه مختصات دو بعدی، ابتدا بُعد xx و سپس بُعد yy را به فرم زوج (x,y)(x,y) مینویسیم. انتخاب حروف xx و yy طبق قرارداد است. معمولاً از حروف کوچک برای متغیرهای نامعلوم و از حروف بزرگ برای مقادیر معلوم استفاده میشود. برای مثال، نقطه PP در شکل ۳، متناظر با مختصات (۳,۵)(۳,۵) است.
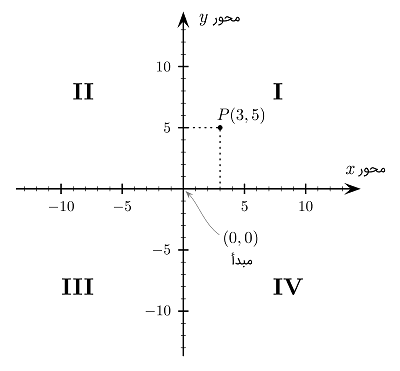
عبور دو محور از یکدیگر، چهار ناحیه را به وجود میآورد که ربع (Quadrant) نامیده شده و معمولاً با عددنویسی رومی I(+,+)I(+,+)، II(−,+)II(−,+)، III(−,−)III(−,−) و IV(+,−)IV(+,−) مشخص میشوند. ربعها با شروع از ربع سمت راست بالا (شمال شرقی) و با حرکت در خلاف جهت عقربههای ساعت نامگذاری میشوند. در ربع اول، هر دو محور مثبت هستند. در ربع دوم، محور xx منفی و محور yy مثبت است. در ربع سوم، هر دو مقدار xx و yy منفی هستند. در ربع چهارم نیز، محور xx مثبت و محور yy منفی است.
دستگاه مختصات دکارتی سه بعدی
دستگاه مختصات دکارتی سه بعدی، سه بعد فضا، یعنی طول، عرض و ارتفاع را مشخص میکند. شکلهای ۴ و ۵، دو نمایش متداول این دستگاه مختصات را نشان میدهد.
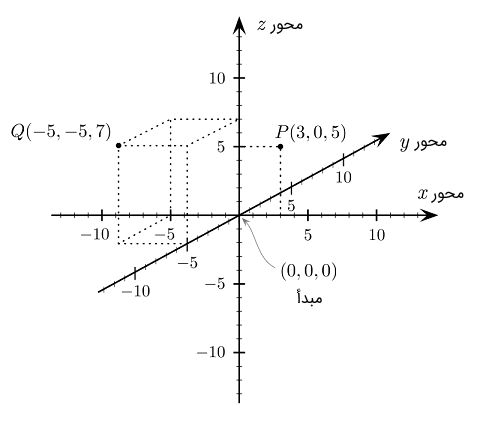
محورهای دستگاه مختصات دکارتی سه بعدی، بر هم عمود هستند. مختصات یک نقطه در این دستگاه، به صورت (x,y,z)(x,y,z) نشان داده میشود. مثلاً در شکل ۴ دو نقطه P(3,0,5)P(3,0,5) و Q(−۵,−۵,۷)Q(−۵,−۵,۷) نشان داده شدهاند.
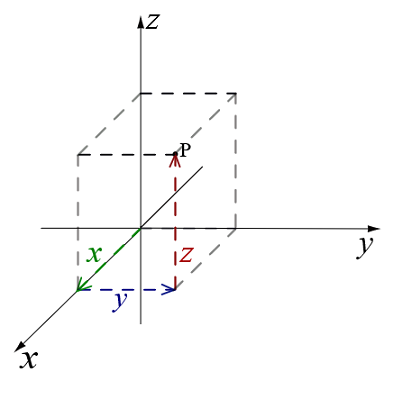
مختصههای xx، yy و zz یک نقطه را میتوان به ترتیب، با فاصله آن از صفحات yzyz، xzxz و xyxy نیز مشخص کرد. شکل ۵، فاصله نقطه PP را از این صفحات نشان میدهد.
صفحات xyxy، yzyz و xzxz، فضای سه بعدی را به هشت قسمت تقسیم میکنند که اصطلاحاً اوکتان (Octant) یا یکهشتم نامیده میشوند. اگرچه در حالت دو بعدی، هر چهار ربع نامگذاری شدند، اما در دستگاه مختصات سه بعدی، فقط اوکتان اول نامگذاری میشود و آن قسمتی است که همه نقاط xx، yy و zz آن مثبت هستند. محور zz در این مختصات، بلندی یا ارتفاع نامیده میشود.
منبع مطالب تکمیلی: faradars
این مطلب چقدر مفید بود؟
به این پست امتیاز دهید!
متوسط آرا ۳ / ۵٫ ۲
اولین نفری باشید که به این پست رای می دهید!








